Динамика гидравлических следящих приводов c дроссельным регулированием
13.2. ДИНАМИКА ГИДРАВЛИЧЕСКИХ СЛЕДЯЩИХ ПРИВОДОВ C ДРОССЕЛЬНЫМ РЕГУЛИРОВАНИЕМ
Динамика ГСП (ДМ). Динамические характеристики и устойчивость такого привода могут быть исследованы как с помощью полной нелинейной системы уравнений или упрощенной нелинейной системы уравнений с учетом уравнения (94), так и с помощью линейных уравнений.
Примечание. Будем в дальнейшем рассматривать ГСП (ДМ) с ГИУ в виде ГЦ как более сложный и более общий случай.
Полная нелинейная система ГСП (ДМ):
1) уравнения сил (90);
2) уравнения расходов (91) и (92) (вместо координаты x используется координата ?x);
3) уравнение обратной связи ?x = x — kocxп где koc — коэффициент обратной связи; koc = a/(a +b);
4) уравнения, учитывающие ограничения по координатам ?x и xп, или уравнения, учитывающие ограничения по dxп/dt и xп;
5) уравнения, учитывающие люфт в кинематической цепи обратной связи.
Полная нелинейная система может быть исследована с помощью аналоговой или цифровой ЭВМ.
Упрощенная нелинейная система уравнений ГСП (ДМ):
Тe же уравнения, что и в случае полной нелинейной системы, но вместо уравнений расходов (91) и (92) рассматривается одно уравнение (94) для скорости выходного звена ГИУ.
Линейная система уравнений ГСП (ДМ):
B этом случае: а) пренебрегаем силами трения РГЦтр и РОРтр; б) не учитываем ограничения по координатам x, dxп/dt и xп и люфт в кинематической цепи обратной связи; в) вместо нелинейных уравнений расходов используем линейное уравнение (98) для скорости выходного звена ГИУ.
Соответствующая структурная схема линейной модели ГСП (ДМ) (для kп ? 0) изображена на рис. 145, а.
Передаточная функция xп/x при PВ= 0
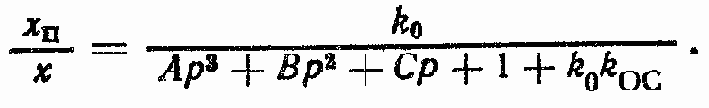
Передаточная функция xп /PВ при x = 0 (см. рис. 145, б):
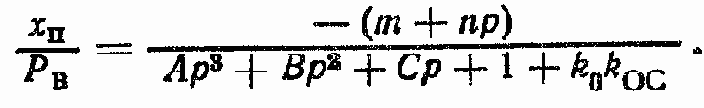
Общее выражение для координаты xп:
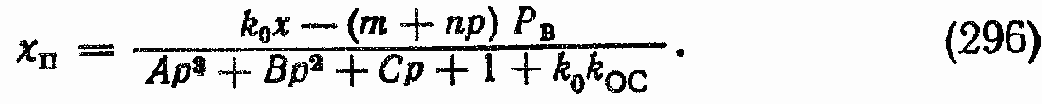
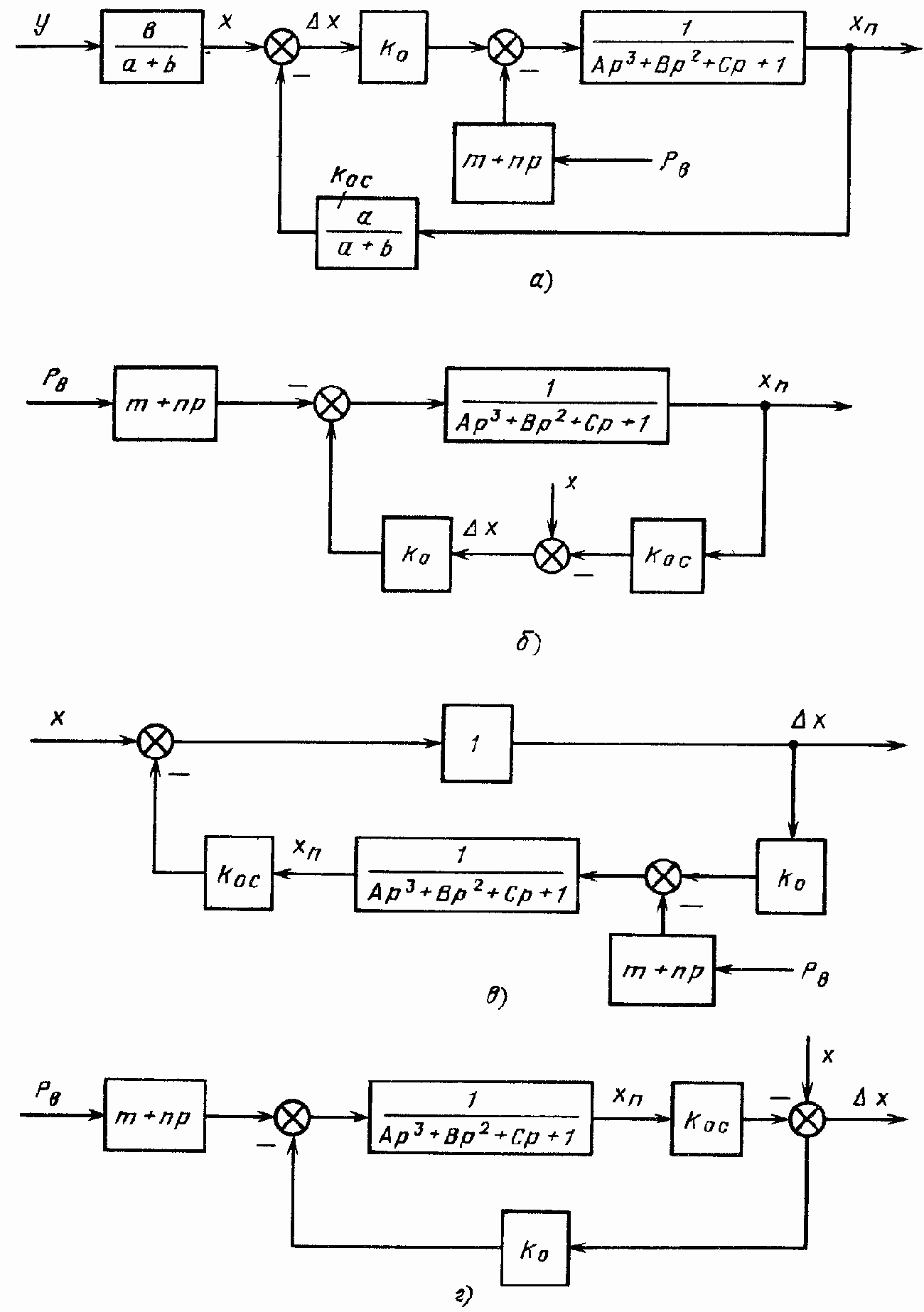
Рис. 145. Структурные схемы ГСП (Д)
Передаточная функция ?x/x при Рв = 0 (см. рис. 145, в):
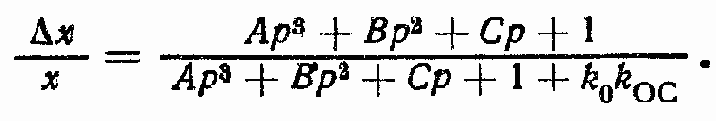
Передаточная функция ?x/Рв при x = 0 (рис. 145, г)
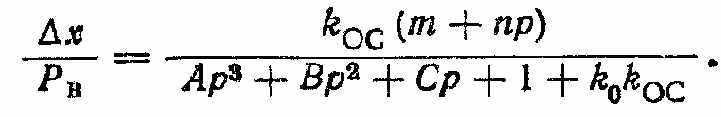
Полное выражение для ошибки
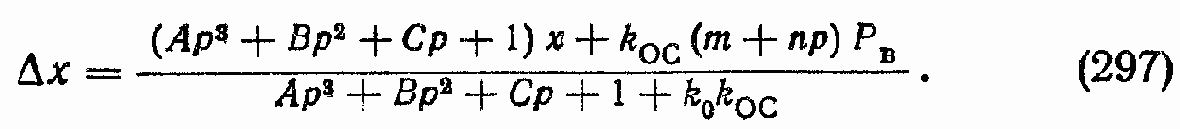
Аналогично рассмотренному выше варианту нагружения ИУ (kп ? 0) можно записать выражение для xп и ?x для случая kп = 0:
14.2. ДИНАМИКА ГИДРАВЛИЧЕСКИХ СЛЕДЯЩИХ ПРИВОДОВ C ОБЪЕМНЫМ РЕГУЛИРОВАНИЕМ
Уравнения ГСП (O). Рассмотрим вначале основные уравнения и передаточные функции ГСП (OM) без МУ как наиболее простой случай (см. рис. 147). Динамические характеристики и устойчивость такого ГСП могут быть исследованы как с помощью полной нелинейной системы уравнений, так и с помощью линейных уравнений.
Полная нелинейная система ГСП (OM):
1) уравнение (85) моментов на валу ГМ;
2) уравнение (86) моментов нагрузки;
3) уравнение (122) расходов;
4) уравнение обратной связи ?? = ? — (1/i2) ?;
5) уравнение связи координат ?? и e: e = kе ??;
6) уравнения, учитывающие ограничения по ?? и ?;
7) уравнения, учитывающие люфт в цепи управления и в цепи обратной связи.
Полная нелинейная система ГСП (OM) может быть исследована с помощью ЭВМ.
Линейная система уравнений ГСП (OM).
В этом случае: а) пренебрегаем моментами трения М??тр и МОРтр; б) не учитываем ограничение по координатам ?? и ?; в) вместо уравнения расходов (122) используется уравнение (126) при Q0 = 0; г) не учитываем люфты в кинематических механизмах.
B соответствии со структурной схемой (см. рис. 147, б) передаточная функция, связывающая координаты ? и ? (для сОР = 0 и при МВ= 0):
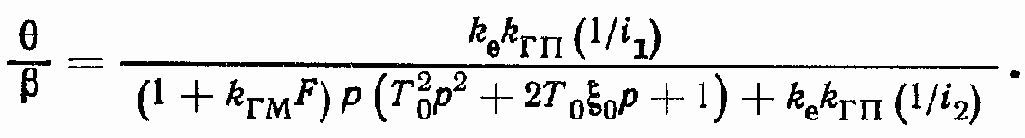
Введем обозначения:
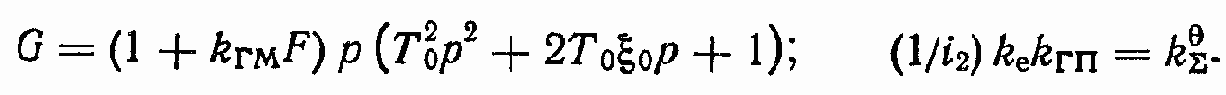
Передаточная функция ?/М? при ? = 0
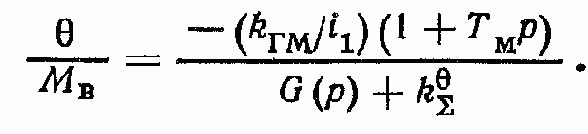
Общее выражение для ?:
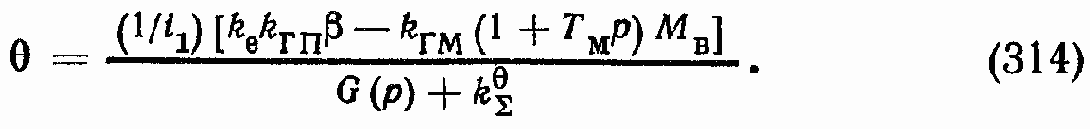
Передаточная функция по ошибке ?? при М? = 0
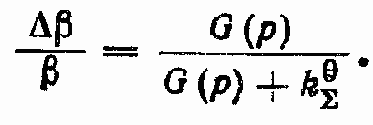
Передаточная функция по ошибке ?? при ? == 0
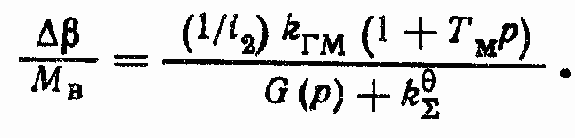
Общее выражение для ошибки
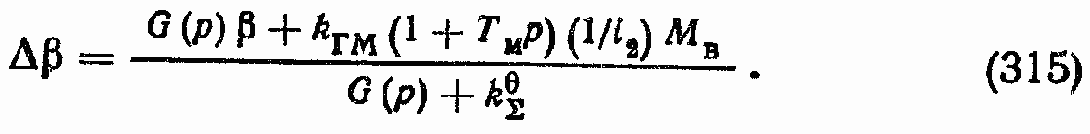
Теперь рассмотрим уравнения ГСП (OM) с механизмом управления (см. рис. 148).
Полная нелинейная система ГСП (OM) с механизмом управления.
1. Уравнения механизма управления. B рассматриваемом случае МУ представляет собой ГСП (ДМ) (см. п. 2 гл. 13), входная координата которого x(p) определяется по уравнению: x =
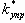
При исследовании динамики ГСП (OM) динамические характеристики МУ аппроксимируют апериодическим звеном
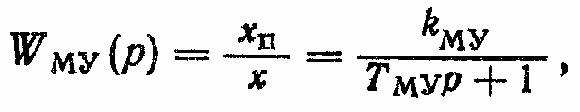
постоянную времени ТМу выбирают по точным ЛАФЧХ в полосе частот, в пределах которой формируется контур ГСП (OM).
Примечание. Выше мы исследовали устойчивость замкнутого контура ГСП (ДМ) без специальных КУ. Известно, что с помощью КУ можно обеспечить устойчивость замкнутого контура ГСП (ДМ) при более гибком варьировании параметров привода и нагрузки. Применение КУ в ГСП и, в частности, применение гидромеханических КУ в ГСП (ДМ) рассмотрено в гл. 8.
Динамика ЭГСП (Д). Нелинейные и линейные уравнения силовой части ЭГСП (Д) ничем не отличаются от соответствующих уравнений ГСП (ДМ). К уравнениям силовой части добавляются уравнения, описывающие динамику преобразующего устройства (ПУ), усилителя мощности, электрогидравлического усилителя мощности и согласующей аппаратуры (если она применяется).
Динамика ЭГУ и усилителя мощности подробно описана в гл. 7. Следует отметить, что при анализе устойчивости и динамических характеристик ЭГСП (Д) динамические характеристики ЭГУ, как правило, аппроксиммируются апериодическим звеном
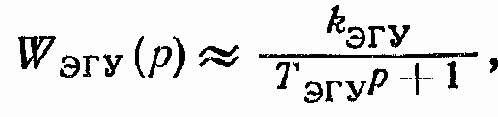
где постоянная времени Тэгу определяется по точным ЛАФЧХ ЭГУ в полосе частот, в пределах которой формируется контур ЭГСП (Д). В нелинейной модели ЭГСП (Д) как основная нелинейность ЭГУ учитывается только ограничение или по выходной координате ЭГУ, или по расходу РЖ, поступающей к ГИУ.
Динамические характеристики усилителя мощности (УМ) с достаточной для инженерных расчетов точностью описываются с помощью апериодического звена (см. п. 4 гл. 6 и п. 4 гл. 7)
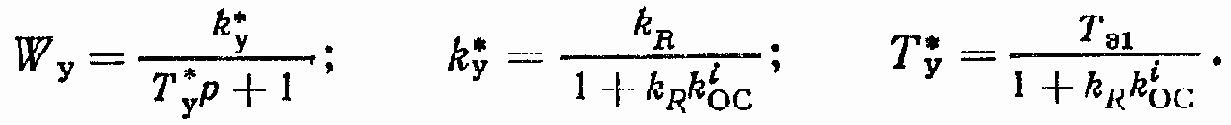
В нелинейной модели УМ как основная нелинейность учитывается ограничение по напряжению в цепи сигнала рассогласования контура УМ, замкнутого обратной связью по току.
Динамические характеристики преобразующего устройства описываются, как правило, линейными дифференциальными уравнениями, вид и порядок которых в основном зависят от типа корректирующего устройства, стоящего в цепи сигнала рассогласования (входящего в состав ПУ).
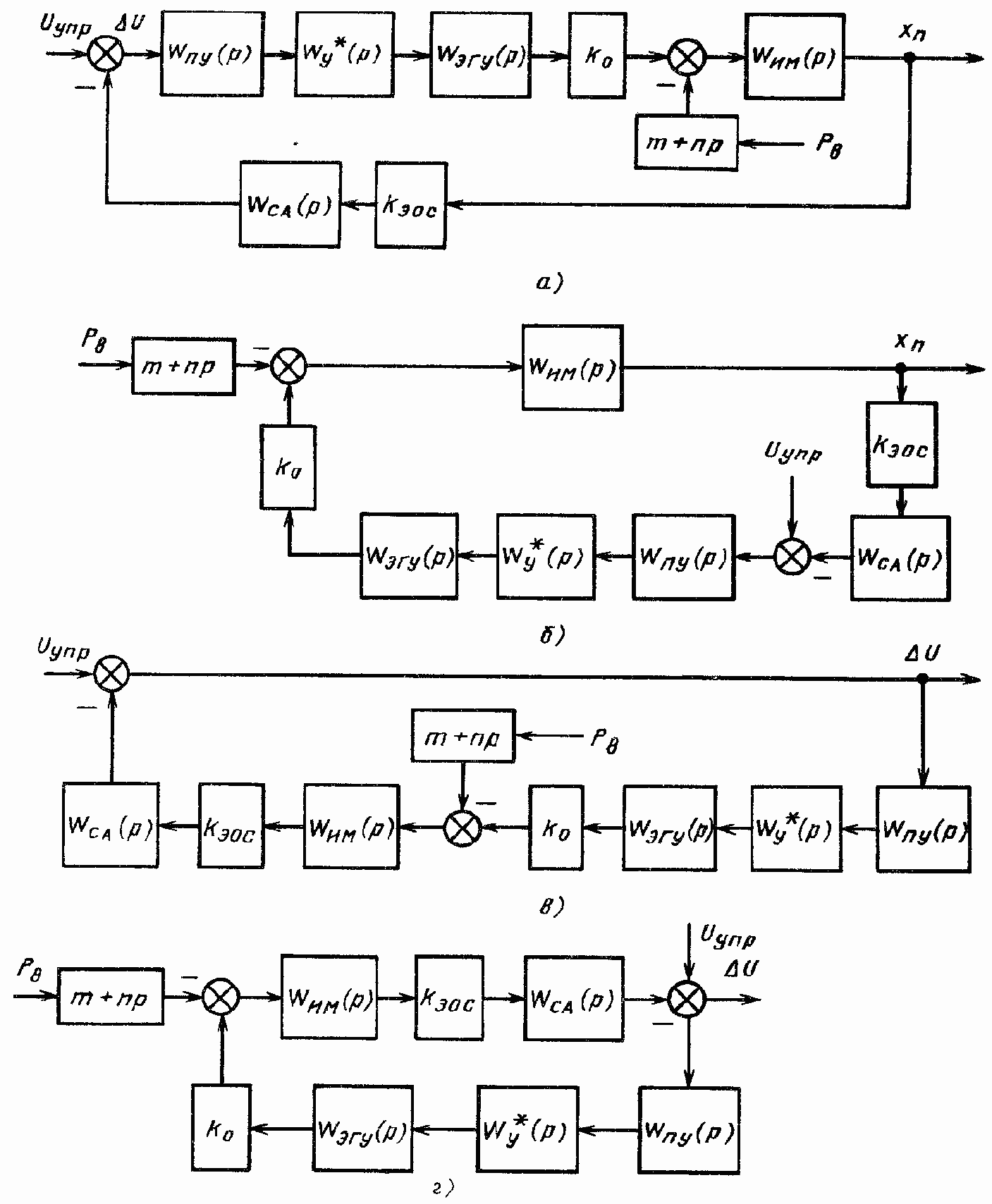
Рис. 146. Структурные схемы ЭГСП (Д)
Динамические характеристики согласующей аппаратуры — это характеристики фазочувствительного выпрямителя (ФЧВ) и частотного фильтра, стоящих в цепи обратной связи от выходной координаты ЭГСП (Д) до устройства вычисления ошибки в случае применения в качестве датчика обратной связи датчика на переменном токе, например индукционного датчика.
Как правило, работа ФЧВ характеризуется его коэффициентом передачи (считается, что в полосе частот формирования контура привода динамические характеристики ФЧВ намного выше динамических характеристик отдельных элементов привода и ими можно пренебречь).
Динамические характеристики частотного фильтра зависят от частоты питающего напряжения индукционного датчика и от типа и схемы фильтра. B большинстве случаев достаточно ограничиться описанием динамических свойств фильтра с помощью апериодического звена с передаточной функцией
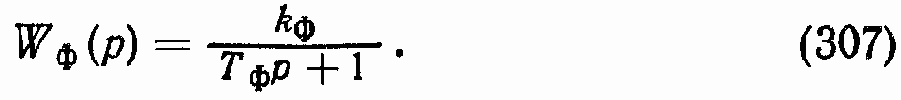
Постоянная времени Тф выбирается по точным ЛАФЧХ фильтра в полосе частот, где формируется контур ЭГСП (Д).
Динамические характеристики ЭГСП (Д) с шаговым двигателем, как правило, исследуют при условии, что входной координатой является угол поворота шагового двигателя, закон движения которого в первом приближении (при пренебрежении динамикой в пределах одного шага) можно записать с помощью линейной функции ?шд = kшдt.
При изучении линейной модели ЭГСП (Д), так же как и при изучении ГСП (ДМ), используют передаточные функции:

Примечание. Без ущерба для изложения сути материала ограничимся в дальнейшем рассмотрением передаточных функций для ЭГСП (Д), структурная схема которого изображена на рис. 142, а.
Передаточная функция xП/Uупр при Рв = 0 (рис. 146, а).
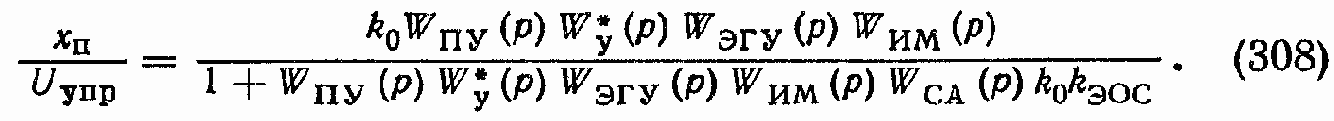
Здесь
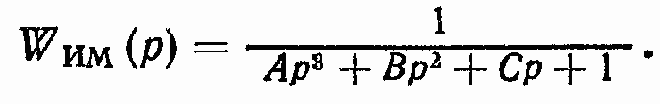
Передаточная функция xП/Рв при Uупр = 0 (рис. 146, б):
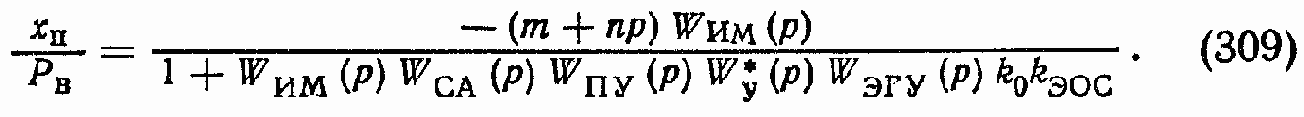
Объединив (308) и (309), получим
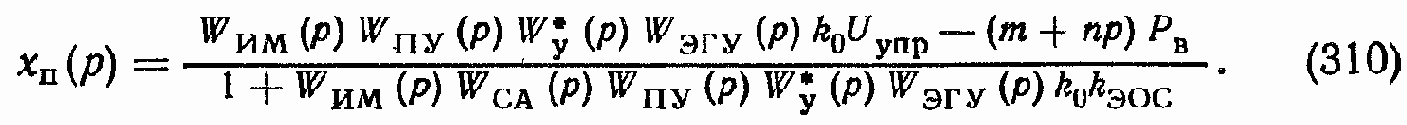
Передаточная функция для ?U(p) может быть записана аналогично передаточной функции для ?x(p) ГСП (ДМ):
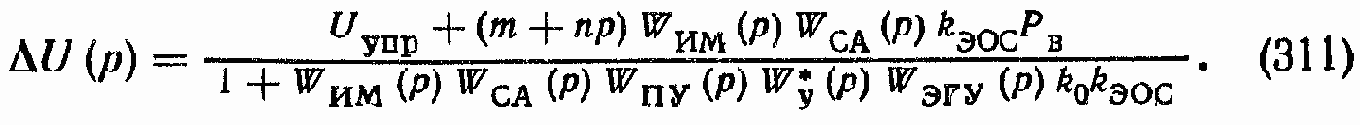
Структурные схемы, соответствующие формуле (311), приведены на рис. 146, в, г.
Если в уравнении сил на ИУ kп = 0 то формулы для xП(p) и ?U(p) примут следующий вид:
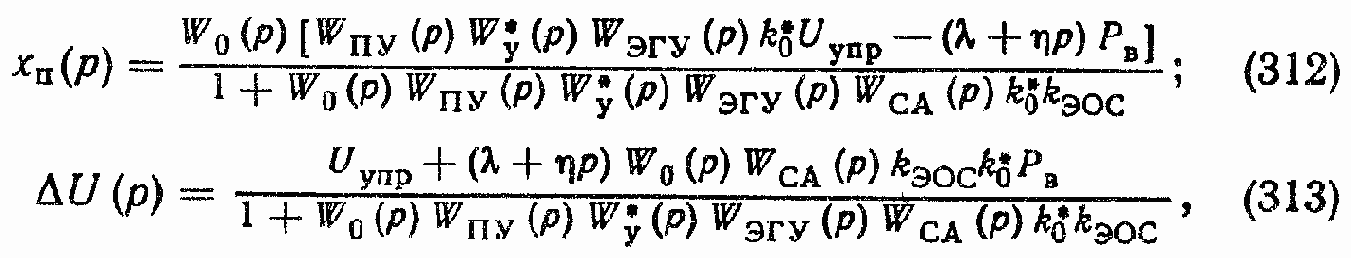
где
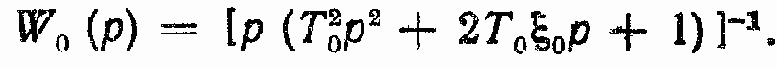
Анализ динамических характеристик, определение необходимого коэффициента усиления контура линейной модели ЭГСП (Д) при обеспечении заданного запаса по устойчивости и исследование статической и динамической точностей проводят по структурным схемам (см. рис. 142). Нужный коэффициент усиления при выбранных элементах ЭГСП (Д) (усилителе мощности, ЭГУ, датчике обратной связи, согласующей аппаратуре) достигается за счет выбора коэффициента усиления преобразующего устройства, которое в самом простом случае представляет собой операционный усилитель.
Как правило, определение устойчивости и исследование динамических характеристик линейной математической модели ЭГСП (Д) проводят путем построения ЛАФЧХ разомкнутого и замкнутого контуров привода. При этом так же, как и в ГСП (ДМ), при определении устойчивости замкнутого контура ЭГСП (Д) в формулах для расчета коэффициентов
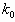
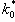
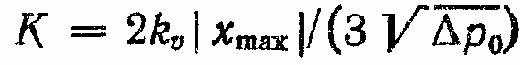
Устойчивость ЭГСП (Д). Все закономерности, выявленные при исследовании устойчивости динамических характеристик ГСП (ДМ), могут быть исследованы для ЭГСП (Д) со следующими дополнениями.
1. Для увеличения запасов устойчивости и улучшения динамических характеристик необходимо уменьшать постоянные времени Tэгу и
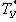
2. Влияние WПУ(p) на устойчивость, статические и динамические характеристики ЭГСП (Д) в случае, когда в состав ПУ входит КУ того или иного типа, весьма существенно, поэтому эти вопросы являются предметом специального рассмотрения в гл. 7.
3. Как сказано выше, динамические характеристики согласующей аппаратуры в случае применения датчика обратной связи на переменном токе описываются с помощью апериодического звена [см. (307)]. Такое звено в цепи обратной связи ЭГСП (Д) уменьшает значение частоты разомкнутого контура, при которой фазовый сдвиг равен 180°, и, следовательно, ухудшает устойчивость. Однако это звено обеспечивает дифференцирующий эффект в замкнутом контуре, что необходимо учитывать при построении ЛАФЧХ разомкнутого и замкнутого контуров ЭГСП (Д).
Назад | Содержание
| Вперед
2. Уравнение (85) моментов на валу ГМ.
3. Уравнение (86) моментов нагрузки.
4. Уравнение (122) расходов.
5. Уравнение связи координат хП и ?: ? == k?хП,
6. Уравнение связи координат ? и e: e = kупр?.
7. Уравнения, учитывающие ограничения по координатам хП, ? и ?.
8. Уравнения, учитывающие люфт в кинематических механизмах по цепи управления и по цепи обратной связи.
Линейная система уравнений ГСП (OM) с МУ.
B этом случае: а) пренебрегаем моментами трения М??тр и МОРтр; б) не учитываем ограничения по координатам хП, ? и ?; в) вместо уравнения расходов (122) используется уравнение (126) при Q0 = 0; г) не учитываем люфты в кинематических механизмах.
Соответствующая структурная схема ГСП (OM) при сОР = 0 приведена на рис. 148, б.
Передаточная функция ?/? при MВ = 0
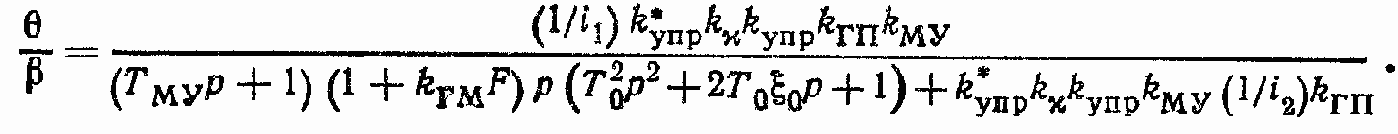
Обозначим
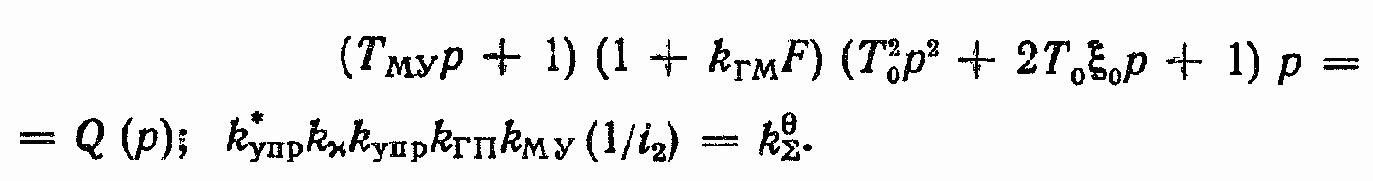
Передаточная функция ?/М? при ? = 0
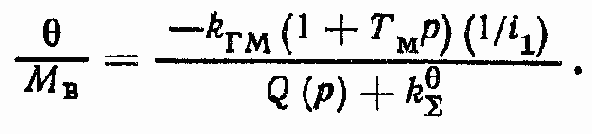
Общее выражение для координаты ?
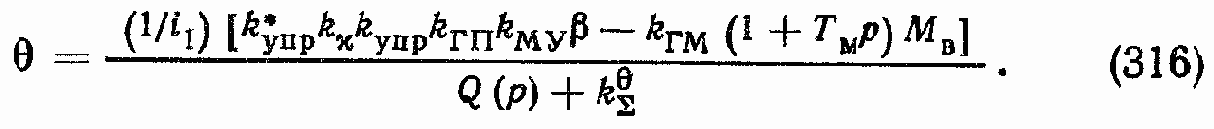
Передаточная функция по ошибке у = ? — ?ОС при МВ = 0
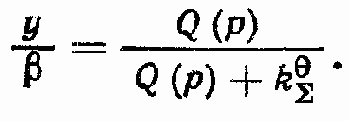
Передаточная функция у/М? при ? = 0
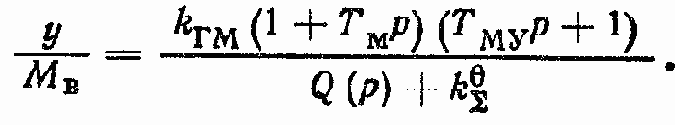
Общее выражение для ошибки
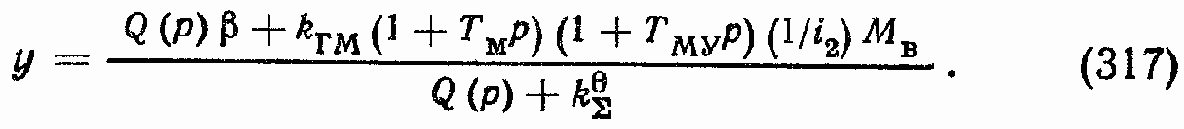
Для случая сОР ? 0 формулы (316) и (317) могут быть записаны в следующем виде:
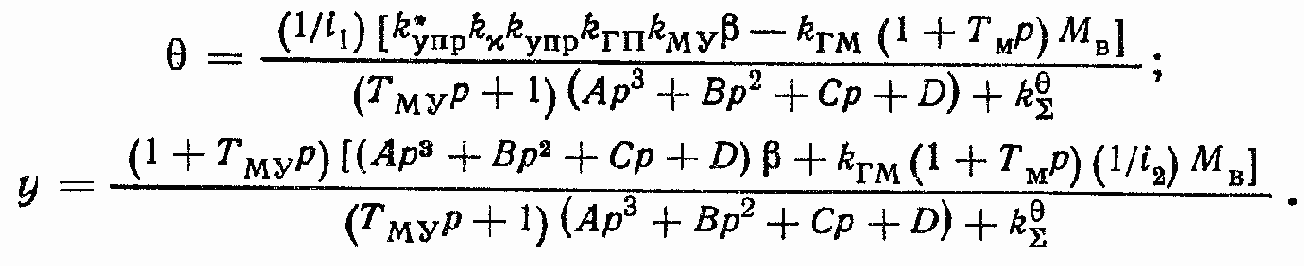
Устойчивость замкнутого контура ГСП (OM). Для выявления принципиальных закономерностей рассмотрим простейший вариант ГСП (OM) — без МУ.
Характеристическое уравнение для сОР = 0
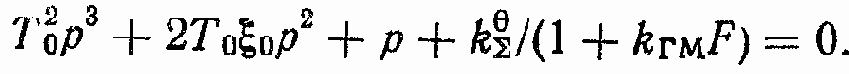
Критерий Гурвица может быть записан в следующем виде:
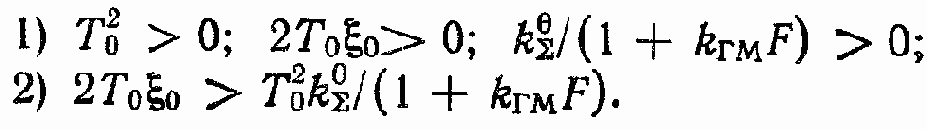
Выполнение первого условия очевидно. Рассмотрим второе условие
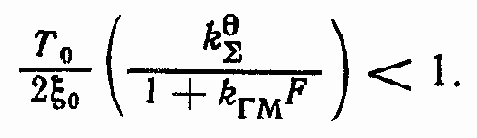
Если подставить в последнее неравенство значение T0, ?0, kгп, kгм (см. гл. 3), то получим
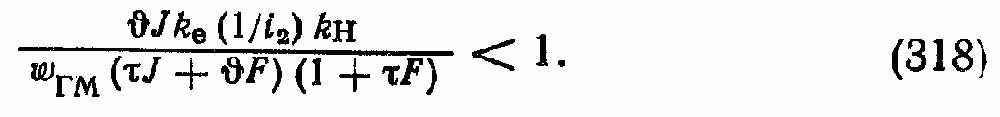
Из последнего неравенства следует, что для повышения запасов устойчивости замкнутого контура ГСП (OM) необходимо:
уменьшать коэффициенты ke, (1/i2) и kH, параметр упругости ? (уменьшать V и увеличивать ??), -инерционную нагрузку (J); увеличивать коэффициент демпфирования (F), параметр герметичности ? (увеличивать утечки и перетечки), рабочий объем ГМ (?гм).
Если рассмотреть случай сОР ? 0, то, введя обозначение
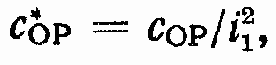
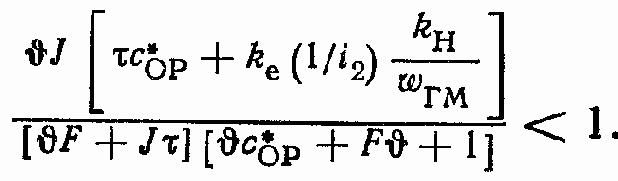
Последнее неравенство, так же как и неравенство (318), позволяет оценить влияние параметров нагрузки и параметров привода на устойчивость замкнутого контура ГСП (OM).
Рассмотрим теперь нелинейные и линейные уравнения ЭГСП(О). Уравнения силовой части ЭГСП (O) ничем не отличаются от соответствующих уравнений ГСП (OM). К уравнениям силовой части добавляются уравнения, описывающие динамику преобразующего устройства, согласующей аппаратуры и уравнения механизма управления. Как и в случае ЭГСП (Д), уравнения преобразующего устройства в зависимости от типа последовательного КУ описываются дифференциальными уравнениями, вид и порядок которых определяется типом КУ. Так как мы условились в данной главе не рассматривать ни параллельные, ни последовательные КУ, то будем считать в дальнейшем преобразующее устройство ПУ простым усилительным звеном с коэффициентом усиления kу. К согласующей аппаратуре обычно относят ФЧВ и частотный фильтр. Так же как и при рассмотрении динамики ЭГСП (Д), будем считать, что динамика фильтра описывается простейшим звеном

постоянную времени которого Тф выбирают по точным ЛАФЧХ фильтра в полосе частот формирования контура привода. ФЧВ будем считать усилительным звеном. Как мы условились выше (при рассмотрении МУ с механической обратной связью), динамические характеристики МУ будем учитывать с помощью апериодического звена

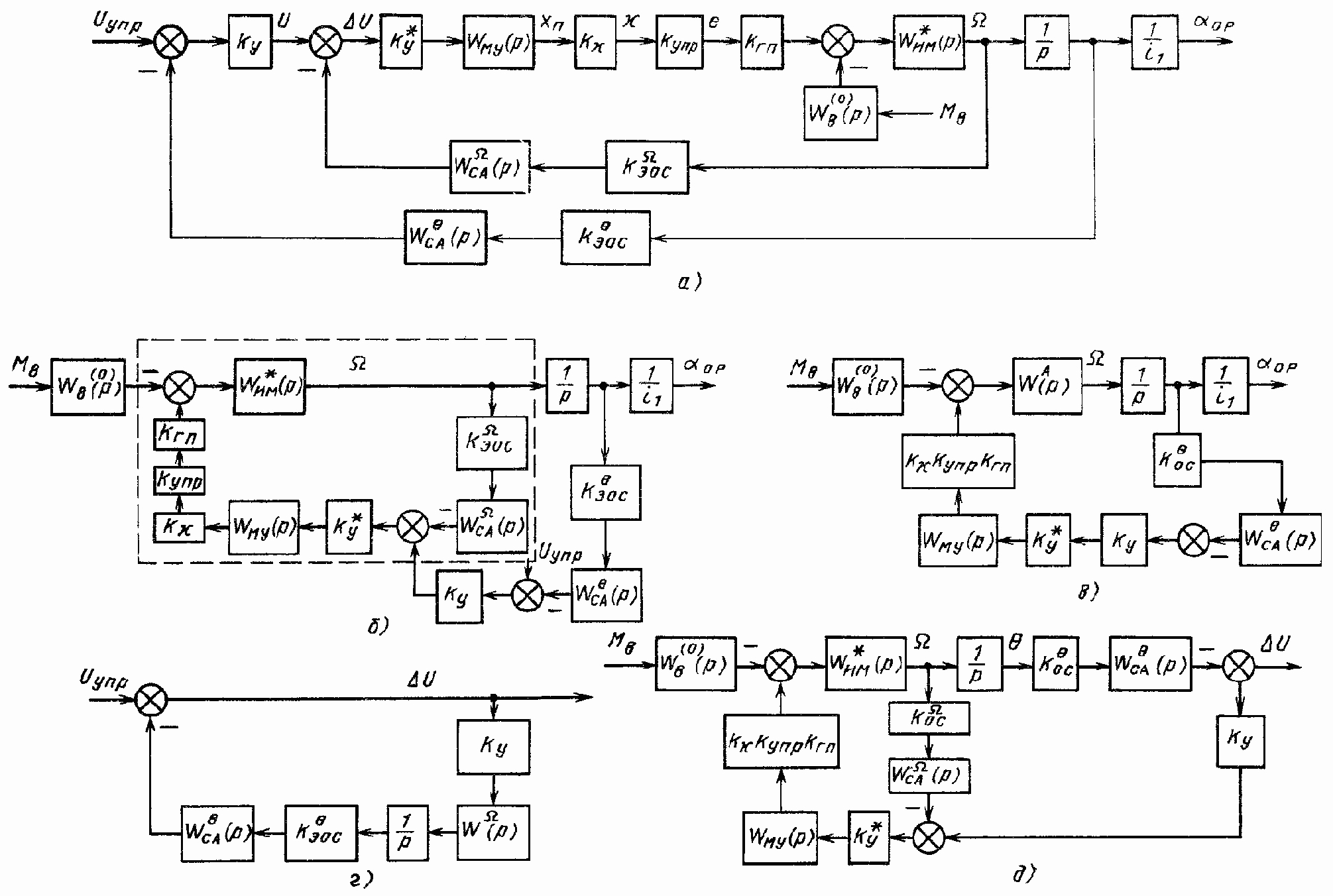
Рис. 152. Структурные схемы ЭГСП (O)
Примечание. B данном случае (применительно к схеме ЭГСП; (O) на рис. 150, 6} под WМУ(р) подразумеваем передаточную функцию части структуры ЭГСП (O) от Uупр (p) до xп (p).
В качестве примера ЭГСП (O) рассмотрим следящий привод, принципиальная схема которого дана на рис. 151, при условии, что сОР = 0. Структурные схемы такого привода с учетом принятых упрощений могут быть представлены так, как показано на рис. 152.
Обозначим
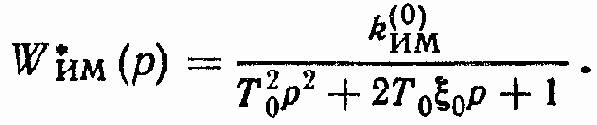
Рассмотрим вспомогательную передаточную функцию
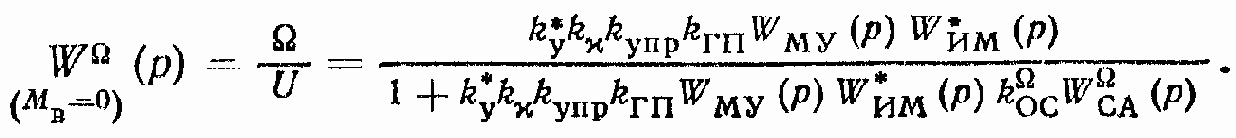
Передаточная функция, связывающая координаты ? и Uупр (рис. 152, а):
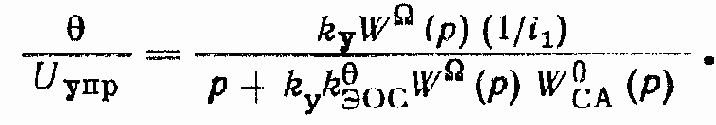
Рассмотрим передаточную функцию ?/М? при Uупр = 0 (рис. 152, б). Введем вспомогательную передаточную функцию
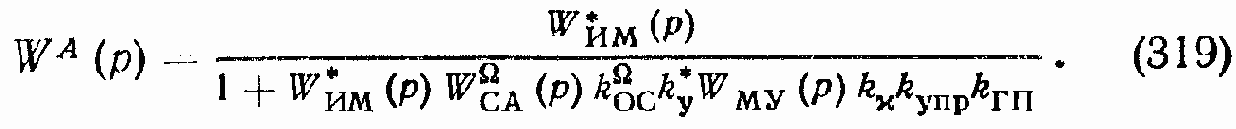
Обозначим
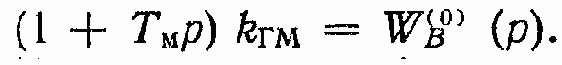
C учетом (319) передаточная функция ?/М? при Uупр = 0 (рис. 152, в) записывается в виде
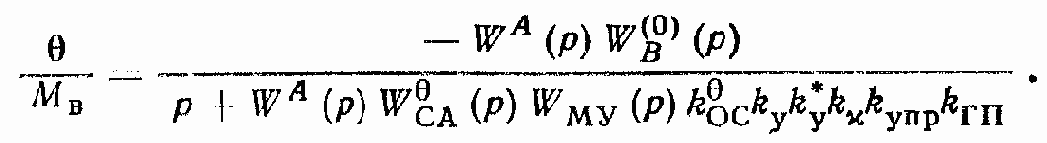
Передаточные функции для ошибки ?U с учетом структурных схем изображенных на рис. 152,г и д, записываются в следующем виде:
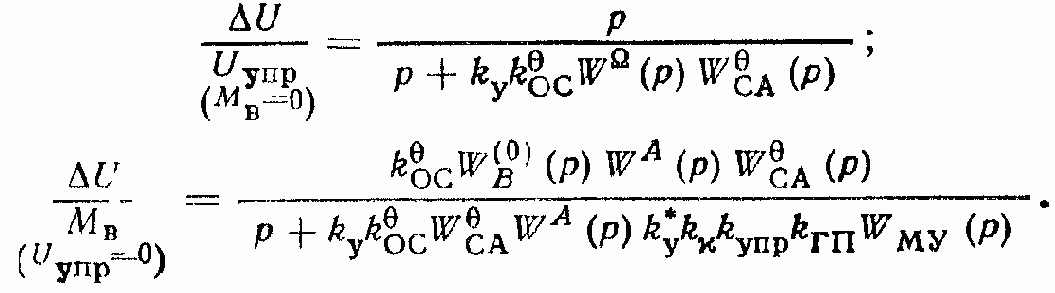
Назад | Содержание
| Вперед