Частотная передаточная функция
Рабочие файлы: [Измерение ЧХ]
Если на вход любой системы подать сигнал синусоидальной формы:
x(t) = Xm cos(wt) = Xm e jwt .
Очевидно, что выходной сигнал будет иметь ту же форму:
y(t) = Ym cos(wt+j) = Ym e j(wt+j) .
Зависимость же между амплитудами и фазами выходного и входного сигналов определяет ДУ движения системы. Возмем произвольное, считая помеху f(t) равной нулю:
(T22 p2 + T1
p + 1) y(t) = (k1 + k2
p) x(t) .
Подставим сигналы в уравнение движения:
T22(jw)2
Ym e j(wt+j) + T1(jw) Ym e
j(wt+j) + Ym e j(wt+j) = k1 Xm e jwt + k2(jw) Xm e
jwt .
Найдем отношение выходного сигнала ко входному:
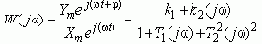
Заметим. Если вместо подстановки сигналов записать ДУ движения системы для домена Лапласа и вновь найти отношение выходного сигнала к входному (а точнее их изображений), то полученная в ходе этого преобразования ПФ совпадет с точностью до свободной переменной с частотной ПФ.
Резюме1: Частотная передаточная функция получается из обычной заменой оператора Лапласа s на комплексную частоту jw, т.е. в результате перехода от изображения Лапласа к изображению Фурье.
Резюме 2: ДУ движения системы связывает входной и выходной сигналы (т.е. функции времени), ПФ связывет изображения Лапласа тех же сигналов, а частотная ПФ связывает их спектры.