Единичная функция. Дельта-функция. Типовые реакции систем
Рабочие файлы: [Интеграл Дюамеля] [Интеграл свертки]
[h(t) & w(t)] [Интеграл свертки]
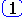
Математическая функция, заданная условиями: 1(t)= 0
при t < 0, и 1(t) = 1 при
t > 0. Для автоматических систем является распространенным видом входного воздействия. Как правило, подобные воздействия сопровождают процессы включения систем и вызывают переходы от одного установившегося состояния к другому.
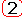
d(t)
Математическая функция, заданная условиями: d(t) ® Ґ
при t = 0, и d(t) = 0
при t № 0, - т.е. это импульс с бесконечной амплитудой, площадь которого принимается равной 1. Для автоматических систем является менее распространенным видом входного воздействия, чем единичная ступенчатая функция. Однако для теоретического описания последних имеет существенное значение. Подобные воздействия характерны для радарных комплексов, описывают передачу импульса при упругом взаимодействии и т.д.
Из определений функций 1(t) и d(t) очевидна связь между ними:
(1)
1(t) = т d(t) dt и d(t) = 1'(t).
Единичная ступенчатая функция 1(t) легка для практической реализации с высокой точностью, однако дельта-функцию Дирака d(t)
реализовать сложнее. Для теоретического описания систем и их моделирования ее можно грубо представить с помощью двух ступенчатых функций:
(2)
d(t) »
N 1(t) - N 1(t-e),
где: N - амплитуда функций, e - время, на которое запаздывает вторая ступенчатая функция, при этом N
e = 1 и e ® 0.
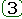
Переходный процесс на выходе типового звена или линейной системы, возникающий при подаче на вход единичной ступенчатой функции 1(t).
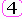
Переходный процесс на выходе типового звена или линейной системы, возникающий при подаче на вход короткого импульса, который, в приближении, можно рассматривать как дельта-функцию Дирака d(t).
В виду независимости присущих линейным системам свойств от внешних воздействий и наличия связи (1) между последними, подобное же отношение существует и для соответствующих типовых реакций:
h(t) = т w(t) dt и w(t) = h'(t).
Докажем эту взаимосвязь подав на систему грубую реализацию дельта-функции (2). В этом случае переходный процесс на выходе можно представить следующей суперпозицией:
y(t) = N h(t) - N
h(t-e),
которая будет являться функцией веса, предел которой (при
e ® 0) будет равен производной от переходной функции:
w(t) = lime®0( e N (h(t) - h(t-e)) / e ) = h'(t), - напомним: N
e = 1.
Функция веса связана с передаточной функцией преобразованием Лапласа:
W(s) = oҐ т w(t) e -st dt.
Переходная функция связана с передаточной функцией преобразованием Карсона:
W(s) = s oҐ т h(t) e -st dt.
Для произвольного входного воздействия, переходный процесс на выходе линейной системы может быть определен на основании интеграла Дюамеля-Карсона, если известны типовые реакции:
h(t): y(t) = x(0) h(t) + ot т x'(t) h(t-t) dt;
w(t): y(t) = ot т
x(t) w(t-t) dt, - так же "Интеграл свертки";
где: t - вспомогательное время интегрирования.