Интегральные оценки качества

Рабочие файлы: [ok_absx_s.vsm]

Интегральные оценки дают обобщенную оценку быстроты затухания и величины отклонения регулируемой величины, в виде единого числового значения.

Находят применение первые три ИТ-оценки из перечисленных в списке:

I1 и I2 - линейные ИТ-оценки (не чувствительны к высшим производным координат САР).

I и I' - квадратичные ИТ-оценки (первая не чувствительна к высшим производным координат САР; вторая – к неподвижному режиму).

I+T12I' - улучшенная квадратичная ИТ-оценка (чувствительна к постоянной и к скоростной составляющим в движении координат САР).

I+T12I'+T24I''+... - ИТ-оценки более высоких порядков (чувствительны к постоянной составляющей в движении координат САР, к их скорости, к ускорению, ...).

Пусть имеем переходные функции h(t).

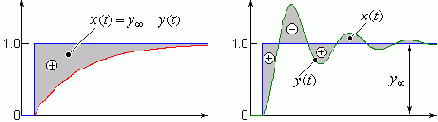
Рассмотрим линейные ИТ-оценки:

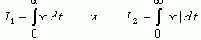
Очевидно, что чем меньше значение оценки I1 или I2, тем лучше переходный процесс, но:

Оценка I1 не может применяться к колебательному переходному процессу.

Аналитическое вычисление оценки I2 по коэффициентам уравнения ошибки затруднено.

Одно значение оценки I2 может соответствовать переходным процессам с разной колебательностью (если совпадают мажоранты и миноранты).

Ограничения "a" и "b" для оценок I1 и I2 преодолеваются квадратичными ИТ-оценками I и I' :

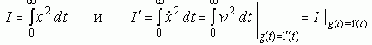
Заметим, что оценку I' можно получить нахождением оценки I, если подать на вход САР не ступенчатую 1(t), а дельта функцию

d(t)=1'(t). Применение оценки I' ограничено тем, что она не чувствительна к установившемуся значению ошибки xҐ.

Ограничение "c" и другие ограничения оценок I1, I2,

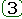
I и I' снимаются улучшенной квадратичной ИТ-оценкой:

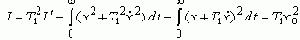
где: x0 - начальное значение отклонения в переходном процессе; I+T12I'

– не формула, а составной символ обозначения данной ИТ-оценки.

Очевидно, что I+T12I'

будет минимальна при T1x'+x = (T1p+1)x = 0. Решение этого ДУ есть экспонента:

, а

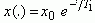
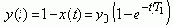
Т.е. улучшенная квадратичная ИТ-оценка I+T12I'

будет иметь минимум при приближении переходной функции к экспоненте с заданной постоянной времени T1.

Можно использовать улучшенные ИТ-оценки более высоких порядков. Например:

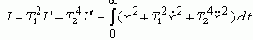
Здесь оценка будет иметь минимум, только при перемещениях координат САР с определенными скоростью и ускорением, которые задаются постоянными времени T1 и T2 соответственно. Идея другого способа выбора параметров оценки заключена в том, что коэффициенты ДУ второго порядка можно выразить в виде затухания z и резонансной частоты q, которыми должна обладать настраиваемая САР.

Содержание раздела