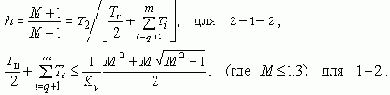О синтезе систем с ЦВМ методом логарифмических амплитудных характеристик

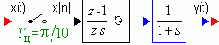
Изображенный дискретный фильтр имеет в области частот
w ЛАЧХ & ЛФЧХ, использовать которые при синтезе неудобно.
Перевод с помощью v-преобразования ЧХ в область псевдочастот l, позволяет получить ЛАЧХ, которые по виду подобны ЛАЧХ непрерывных систем.
Последовательность преобразований следующая:
Wэ(s)ЧW(s) ® W(z) ®
W(v) ® W(jlTц/2).
Эти преобразования при использовании экстраполятора нулевого порядка могут быть формализованы. Пусть ПФ непрерывной части имеет вид:
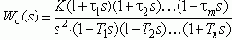
Техническая реализуемость систем с ЦВМ позволяет ввести положения:
Пусть для частоты среза непрерывной части выполняется условие
wср < 2/Tц.
Все постоянные времени знаменателя разделим на две группы - до и после диапазона от частоты среза до частоты дискретизации:
T1, ..., Tq > (1/wср
... 1/wц) > Tq+1, ..., Tn.
Постоянные времени в числителе t1, ...,
tm пусть больше чем 1/wср.
Поскольку система должна быть устойчива, пусть наклон ЛАЧХ на wср
будет -20 дБ/дек.
Принятые положения, позволяют описать свойства систем в области низких и высоких частот двумя ПФ:
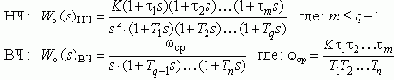
Теперь для формального перехода в область псевдочастот
l (минуя промежуточные z и v-преобразования) достаточно подставить в ПФ Wo(s)НЧ
вместо s jl и умножить ее на множитель (1-jlTц/2), для низких частот приближенно равный 1.
А ПФ Wo(s)ВЧ будет соответствовать выражение:
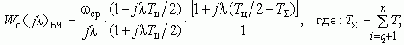
Модуль которого:
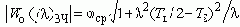
Результирующий фазовый сдвиг обеих областей:

Резюме:
В области НЧ (w < 2/Tц) асимптотическая ЛАЧХ системы с ЦВМ практически сливается с ЛАЧХ непрерывной части (множитель (1-jlTц/2) » 1)
и можно положить l » w. Это позволяет один к одному использовать разработанную для непрерывных систем методику формирования НЧ части желаемой ЛАЧХ.
В области ВЧ отличия вносит множитель (1-jlTц/2), ухудшающий условия устойчивости. Поэтому при формировании запретной ВЧ области в расчетных формулах величина Tц/2 должна быть просуммирована с малыми постоянными времени: